Lernauftrag 29: Auswirkungen der Neutralleiterunterbrechung ermitteln
Hier findest du die Aufgaben ohne Lösungen.
Die Neutralleiterunterbrechung in der Verteilung der Elektroanlage bei einem Kunden führt zu folgendem Problem:
Werden Herdplatte und Elektrobackofen gleichzeitig eingeschaltet, wird die Beleuchtung in der Küche erheblich heller, was mitunter zur Zerstörung der Glühlampen führt.
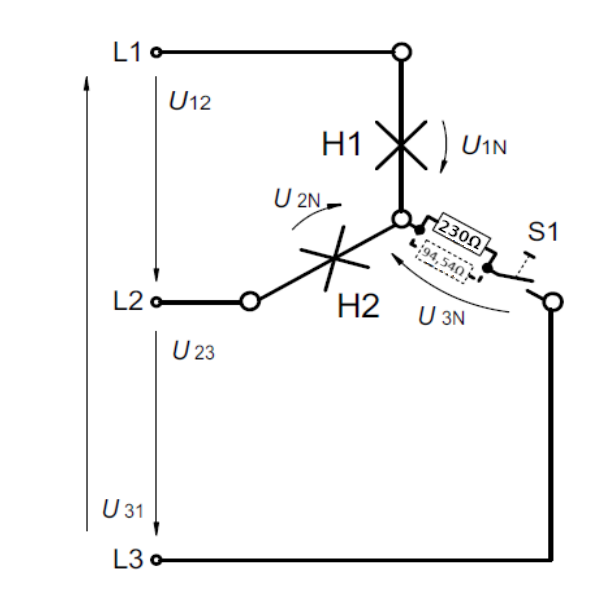
- Drehstromsystem: \(400\ V/230\ V\)
- Glühlampen: \(230\ V/100\ W\)
- Herdplatte: \(230\ \Omega\)
- Backofen: \(94,54\ \Omega\)
Aufgabe 1
Ermittle die in der Tabelle fehlenden Werte:
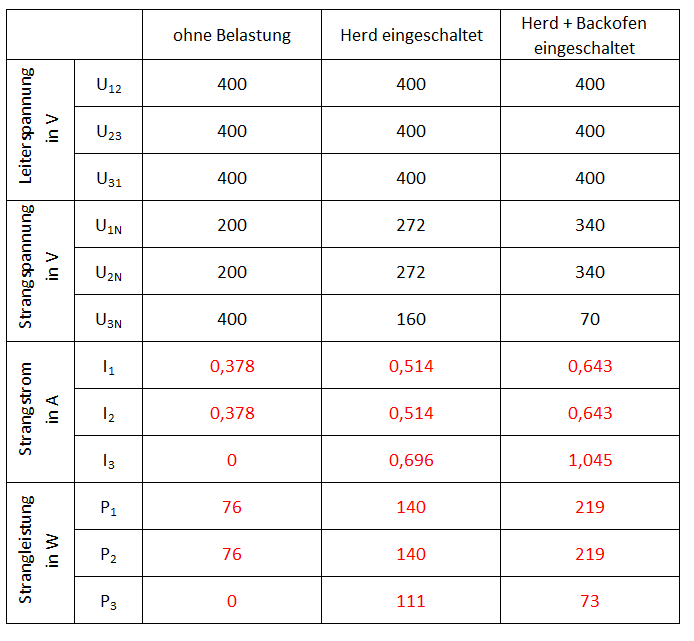
Berechnungen der Werte
Zuerst der Widerstand der Lampen H1, H2:
geg: \(P=100\ W, U=230\ V\)
ges: \(R_{H1}, R_{H2}\)
Lös: \(R_{H1}=R_{H2}=\frac{U^2}{P}=\frac{(230\ V)^2}{100\ W}=529\ \Omega\)
ohne Belastung
\(I_1=\frac{U_{1N}}{R_{H1}}=\frac{200\ V}{529\ \Omega}=0,378\ A\)
\(I_2=\frac{U_{2N}}{R_{H2}}=\frac{200\ V}{529\ \Omega}=0,378\ A\)
\(I_3=0\ A\), offene Klemme => kein Stromfluss
\(P_1=\frac{U_{1N}^2}{R_{H1}}=\frac{(200\ V)^2}{529\ \Omega}=76\ W\)
\(P_2=\frac{U_{2N}^2}{R_{H2}}=\frac{(200\ V)^2}{529\ \Omega}=76\ W\)
\(P_3=0\ W\), offene Klemme => kein Stromfluss => keine Leistung
Herd eingeschaltet
\(R_{\mathrm{Herd}}=230\ \Omega\)
\(I_1=\frac{U_{1N}}{R_{H1}}=\frac{272\ V}{529\ \Omega}=0,514\ A\)
\(I_1=\frac{U_{1N}}{R_{H1}}=\frac{272\ V}{529\ \Omega}=0,514\ A\)
\(I_3=\frac{U_{3N}}{R_{\mathrm{Herd}}}=\frac{160\ V}{230\ \Omega}=0,696\ A\)
\(P_1=\frac{U_{1N}^2}{R_{H1}}=\frac{(272\ V)^2}{529\ \Omega}=140\ W\)
\(P_2=\frac{U_{2N}^2}{R_{H2}}=\frac{(272\ V)^2}{529\ \Omega}=140\ W\)
\(P_3=\frac{U_{3N}^2}{R_{\mathrm{Herd}}}=\frac{(160\ V)^2}{230\ \Omega}=111\ W\)
Herd+Backofen eingeschaltet
Kombinierter Widerstand aus Herd und Backofen:
\(R_\mathrm{beide}=\frac{R_{\mathrm{Herd}}\cdot R_{\mathrm{Ofen}}}{R_{\mathrm{Herd}}+ R_{\mathrm{Ofen}}}=\frac{230\ \Omega\cdot 94,54\ \Omega}{230\ \Omega+94,54\ \Omega}=67\ \Omega\)
\(I_1=\frac{U_{1N}}{R_{H1}}=\frac{340\ V}{529\ \Omega}=0,643\ A\)
\(I_1=\frac{U_{1N}}{R_{H1}}=\frac{340\ V}{529\ \Omega}=0,643\ A\)
\(I_3=\frac{U_{3N}}{R_{\mathrm{Beide}}}=\frac{70\ V}{67\ \Omega}=1,045\ A\)
\(P_1=\frac{U_{1N}^2}{R_{H1}}=\frac{(340V)^2}{529\ \Omega}=219\ W\)
\(P_2=\frac{U_{2N}^2}{R_{H2}}=\frac{(340\ V)^2}{529\ \Omega}=219\ W\)
\(P_3=\frac{U_{3N}^2}{R_{\mathrm{Beide}}}=\frac{(70\ V)^2}{67\ \Omega}=73\ W\)
Aufgabe 2
Stelle die Auswirkung der einzelnen Belastungsfälle als Zeigerbild dar.
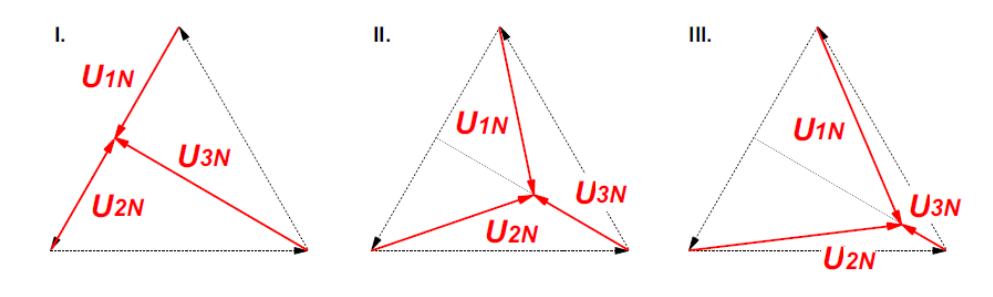
Aufgabe 3
Beschreibe die Ursache für die Helligkeitsänderung.
Der Stangwiderstand der Parallelschaltung von Kochplatte und Backofen hat mit \(67\ \Omega\) den kleinsten Widerstanswert. Über diesem Ersatzwiderstand tritt nur eine kleine Strangspannung auf. Da die Stränge verkettet sind, erhöht sich die Spannung über den beiden anderen Strängen. Der Sternpunkt verschiebt sich.
Aufgabe 4
Da der Widerstandes des Herdes noch geringer ist, wird noch mehr Leistung über die Lampen gehen und sie würden mit sehr hoher Wahrscheinlichkeit schon beim ersten Einschalten des Herdes durchbrennen. In Konsequenz würde auch der Herd nicht mehr gehen, da nun alle Stränge offene Klemmen sind.